Relative Häufigkeit

Definition

Ein Experiment, dessen Ausgang nicht vorhersagbar ist, heißt Zufallsexperiment.
Das Werfen eines Würfels oder das Werfen einer Münze sind Beispiele für Zufallsexperimente.

 
Beispiele

Ein Würfel wird 40-mal geworfen, mit folgendem Ergebnis

Augenzahl	1	2	3	4	5	6
Absolute Häufigkeit	3	7	8	9	5	8
Relative Häufigkeit	0,075	0,175	0,2	0,225	0,125	0,2

Dabei bedeutet die Angabe der absoluten Häufigkeit in der 2.Zeile, wie oft die einzele zahl geworfen wurde (z.B. eins wurde 3-mal geworfen).

Unter der in der 3.Zeile aufgeführten relativen Häufigkeit verstehen wir den Quotienten aus absoluter Häufigkeit und Anzahl der Versuche:

relative Häufigkeit =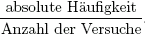  

Zur Kontrolle, ob wir die relativen Häufigkeiten richtig berechnet haben, addieren wir alle relativen Häufigkeiten...

0,075 + 0,175 + 0,2 + 0,225 + 0,125 + 0,2 = 1

...und man erhält die Zahl 1.

Merke Die Summe aller relativen Häufigkeiten ergibt 1.

Wir wollen noch die relative Häufigkeite für das Werfen einer Primzahl berechnen.

Weil 2, 3 und 5 die einzigen Primzahlen kleiner oder gleich 6 sind, ergibt sich für die absolute Häufigkeit des Werfens einer Primzahl 7 + 8 + 5 = 20.
(schau noch einmal auf Tabelle oben, dort findest du die Zahlen)

Also ist die gesuchte relative Häufigkeit